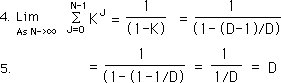Proof H: Number String's Living Average & Directional when A = 1
H0. In the prior article, we derived some important Number String Theorems. The current article provides proofs for some more Number String Theorems. These theorems don't apply to every data stream. They only apply to Number String Data Streams, a small subset of the entire set of data streams. Number String Data Streams are notable in that they consist of identical elements.
H1. The Number String's Living Average Theorem (Eq. E10):
![]()
H2. For each point, N, the right side of the expression is a different constant. For this reason we give this constant a subscript, CN bar. The bar indicates that it is the constant, C, for the Living Average. While everchanging, this constant, CN bar, is not influenced in any way by A, the contents of the Number String data stream.
![]()
H3. Substituting H2 into H1, we arrive at the following equation.
![]()
H4. The Number String's Directional Theorem (Eq. F12):
![]()
H5. As before, the right side of the expression is a different constant for each point, N. For this reason, we give this constant a subscript, CN arrow. The arrow indicates that it is the constant, C, for the Directional. While everchanging, this constant, CN arrow, is not influenced in any way by A, the contents of the Number String data stream.
![]()
H6. Making the proper substitutions (H5 into H4) yields the following expression.
![]()
H7. If A equals 1, it drops out of both equations, H3 and H6.
![]()
H8. The Living Average, the 1st derivative, is a function of its place, N, in the Number String data stream.
![]()
H9. Similarly, the Directional, the 2nd derivative, is a function of its place, N, in the Number String data stream.
![]()
Proof I. The Living Average's Limit = the Number String's Content, A.
Let us now examine what happens to our constants as N, the number of trials (iterations), becomes larger and larger. More specifically, what happens to these constants at the end of the Pulse.
I0. Let's start with the Number String's Living Average, the 1st derivative, XN bar. (Eq. H3)
![]()
I1. Equation E10 provides the algebraic expression for the constant in the Living Average equation, CN bar.
![]()
I2. The Numerator of the fraction can be written the following power series:
![]()
I3. A common calculus theorem states that:
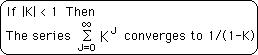
I4&5. K is less than 1 because D-1 is less than D. So our power series converges to 1/(1-K). With a little algebra our proof is complete.
I6. In other words, as N gets larger and larger, the numerator of Equation I1 approaches D, the Decay Factor.
![]()
I7. Applying the above information to Equation I1, yields the following result. As the number, N, of Living Algorithm iterations increases the Living Average Constant approaches 1.
![]()
I8. Applying the above information to Equation I0, yields the following important result, Theorem I. As N, the number of Living Algorithm iterations, increases, the Number String's Living Average approaches A, the Number String's content. In other words, the Living Average approaches the information contained in the Number String at the end of the Pulse. Further, it remains there forever, unless there is some kind of change in the information.
![]()
Proof J. The Limit of the Number String's 1st Directional = 0.
J1. Let's employ this same process to see what happens to the Number String's Directional as the Living Algorithm's iterations rise. Equation H6 provides us with the general expression for the Number String's Directional, XN arrow.
![]()
J2. Equation F12 provides the algebraic expression for the constant in the Directional equation, CN arrow.
![]()
J3. Equation G10 provides an alternate version for KN.
![]()
J4. Equation I6 shows us that the numerator of the above fraction approaches D, as N becomes increasingly larger. Applying this value to the above equation, shows that KN approaches 0 as N grows larger.
![]()
J5. We then apply this information to Equation J2. The Directional's Constant approaches 0, as N, the number of Living Algorithm iterations, increases.
![]()
J6. Applying this information to Equation J1, yields the following equality.
![]()
J7. Simplifying leads to the following very important theorem. Theorem J states that the Number String's Directional approaches 0, as the number, N, of Living Algorithm iterations increases. In other words, the Directional approaches 0 at the end of the Pulse. Further, it remains at 0 forever, unless there is some kind of change in the content of the Number String, its information.
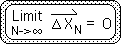
Proof K. The Limit of the Number String's 2nd Directional = 0.

K1. Theorem J states that the Number String's 1st Directional approaches 0, as N, the number of Living Algorithm iterations increases. This proof is intended to establish that the Number String's 2nd Directional also approach 0, as N approaches infinity. The definitional equations for the first 2 Directionals are at right. We also include the Living Average to illustrate the parallel structure. (For economy of expression, we shifted the location of the exponent from our original derivations in the Data Stream Momentum Notebook. However, the two versions, while not exactly the same, are equivalent.)
K2. The Change Series, denoted by the triangle without a hat, is defined as follows.
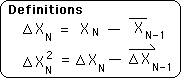
K3. A simple substitution yields the following equation.
![]()
K4. Substituting Equation K3 into the expression for the equation for the 2nd Directional in Equation K1 produces:
![]()
K5. To simplify our analysis, let SN represent the 1st part of the right side of the equation.
![]()
K6. Let's see what happens to SN as N grows larger, i.e. approaches infinity. In the Number String Data Stream the elements, XN, are identical, A. Theorem I (Eq. I8) states that the Living Average, XN bar, approaches A as N approaches infinity. Theorem J (Eq. J7) states that the first Directional, XN arrow , approaches 0 as N approaches infinity. Making these substitutions yields:
![]()
K7. Performing the computations, we see that SN approaches 0 as a limit, as N approaches infinity.
![]()
K8. Substituting SN, K5, into the equation K4 yields an alternate algebraic expression for the 2nd Directional:
![]()
K9. As N approaches infinity, SN approaches 0, hence drops out of the equation. This leaves us with the following simplification.
![]()
K10. To uncover the limit of this equation, let us write the 2nd Directional in yet another form. We start with the assumption that the initial 2nd Directional, X0 arrow 2 , equals 0. This has been a standard assumption that has to do with zeroing out, or taring, the System of extraneous noise.
![]()
K11. Equation K8 provides the 2nd Directional's 1st point (N=1). The second part of the equation drops out due to our prior assumption, K10.
![]()
K12. Equation K8 provides the 2nd Directional's 2nd point (N=2). Substituting the results from K11 yields the following:
![]()
K13. Equation K8 provides the 2nd Directional's 3rd point (N=3). We first substitute the results from K12 and then multiply through by K.
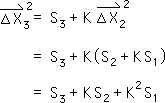
K14. The logical pattern is evident. A simple inductive proof would show the following expression to be true.
![]()
K15. Equation J4 showed that as N approaches infinity that KN approaches 0.
![]()
K16. What is the limit of Equation 14, the 2nd Directional, as N approaches infinity?
![]()
K17. From Equation K7, we know that SN approaches 0 as a limit, as N approaches infinity. From Equation K15, we know that KN also approaches 0, as N approaches infinity. Performing these substitution yields the following result.
![]()
K18. In other words, the end of the right half of the equation shrinks due to K's increasing exponent, while beginning of the equation's right half shrinks due to S's increasing subscript. The result of this double shrinkage is straightforward. As N, the number of Living Algorithm iterations increases, the Number String's 2nd Directional approaches 0 as a limit. This is Theorem K.
![]()
Proof L. The Change Series written in terms of the Directionals & the Data
L1. Theorem K states that the Number String's 2nd Directional approaches 0 as a limit, as N, the number of Living Algorithm iterations, increases. We now want to prove that all the Number String's Directionals approach 0 as a limit. Below is the definitional equation for the general Directional.
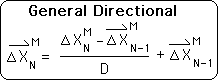
L2. We break the fraction in L1 into 2 parts.
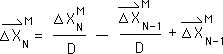
L3. We factor out the like terms, the previous Directional, from the last two elements of the equation.
![]()
L4. Below is the definitional equation for K, the Scaling Factor.
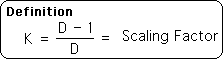
L5. Substituting K into L4 yields the following expression. This is the working equation for the General Directional.
![]()
L6. The following series of equations exhibits the common pattern behind all the Directionals, the Xs with arrows for hats. We include the Living Average, the X with a bar for a hat, to show that it is the original member of the series, when M = 0.

L7. The ∆Xs with arrows for hats are the Directionals. The ∆Xs without hats are members of the Change Series. Below are the definitional equations for the Change Series. We include the first two members of the series to help identify the pattern.
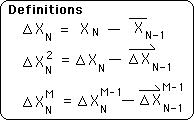
L8. Employing this definition, we would like to test the following hypothesis, an alternate expression for the elements of the Change Series.
![]()
L9. We induced this pattern after examining the individual examples. Equation K3 provides the particular expression when M=2.
![]()
L10. Employing the definitional equation, L7, we obtain the expression for the Change Series when M=3.
![]()
L11. We substitute L9 into L10 to obtain the following expression. The perfect fit with the general expression that we are testing provides another individual example.
![]()
L12. To complete our Inductive Proof, we need to show that the underlying logic of the general expression for the Change Series (L8 with M as the exponent), generates the next member of the Change Series (M+1 as the exponent). The expression for the next member of the series is shown below.
![]()
L13. We isolate the last member of the summation.
![]()
L14. The first 3 elements on the right side of the equation are the same as our Mth member of our Change Series, Equation L8. We perform the substitution.
![]()
L15. Equation L14 is the expression for the M+1 member of our Change Series, as defined by the following expression from Equation L7.
![]()
L16. This completes the proof. Our individual examples generated the pattern. The logical extension of the general expression leads to a known entity. As such, we can safely assume that the general expression that we were testing, Equation L8, is true. This expression is shown below, highlighted as Theorem L, an alternate expression for the Change Series.
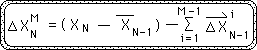
Proof M. An Alternate General Expression for the Mth Directional
M1. We start with the operational equation for the Mth Directional, Eq. L5.
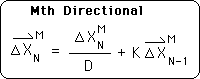
M2. To simplify the expression, we assign S with a subscript of N and a superscript of M to the first term on the right side of the equation.
![]()
M3. Substituting this abbreviation in Equation M1 yields:
![]()
M4. Let's see what happens to the individual cases. We begin by initializing the process. We assume that all the initial Directionals, when the subscript is 0, equal 0. This is the ultimate zeroing out of the System, or taring the System of extraneous noise.
![]()
M5. To see what happens in the 1st case, we substitute 1 for N in Equation M3. The final term in the expression drops out due to our original assumption, M4.
![]()
M6. We extend the process to the 2nd point, N=2 in M3. We substitute the above result into the equation to obtain the following result.
![]()
M7. Moving forward to the 3rd point, we substitute 3 for N (N=3) in the general equation (M3), M1. We then substitute the above result into the equation. We then multiply through by K to obtain the following:
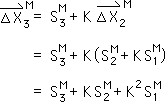
M8. From these particular cases, we induce the following pattern.
![]()
M9. We simplify the expression by writing it as a power series.
![]()
M10. To see if our induction is true, we extend the pattern to the N+1 term. If our induced pattern is true, the following expression should also be true. (N is replaced by N+1 in Equation M9).
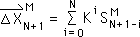
M11. We expand this equation in similar fashion to Equation M8, replacing all the Ns by N+1.
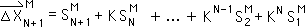
M12. We then factor out a K from the right side of the equation.
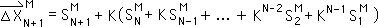
M13. The power series on the right hand side of the equation is the expression for the Mth Directional from Equation M9. This is the general pattern that we inferred was true from the particular cases. We replace the power series with the Mth Directional. This is the definitional expression for the N+1 term that we know to be true from Equation M3.
![]()
M14. We induced the following pattern from individual cases, M5, M6 and M7. We then showed that the general logic behind this pattern led necessarily (deductively) to the next element in the series. We can conclude that our induced pattern is true for all integers. In this fashion, we have elevated the induced pattern to the absolute certainty of a deductive theorem. Following is Theorem M, an alternate expression for the Mth Directional.
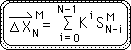
Proof N. The Limit of the Number String's Directionals = 0.
N1. We finally have all the theorems that we need to prove: that as N approaches infinity, the Limit of the Number String's Directionals is 0. We are going to employ another inductive proof.
![]()
N2. Theorems J and K provide specific examples (N=1 and N=2) where the above equation is true.
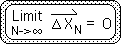
![]()
N3. To complete the inductive proof, we must now show that Equation N3 follows necessarily from Equation N1. In other words, if N1 is true, that N3 is also true. We can deduce the next element (N+1) in the series from the prior element (N).
![]()
N4. Theorem M provides us with a starting point. We show the theorem's expanded version (Equation M8) below.
![]()
N5. Now let us write Theorem M for the M+1 term in the series. We know this statement to be true, as it is an extension of the theorem.
![]()
N6. Equation J4 showed that KN approaches 0, as N approaches infinity.
![]()
N7. When N approaches infinity, the last terms of the right hand side of the equation also approach 0 (Equation N5 above).
![]()
N8. As N approaches infinity, what limit does the left hand side of the equation approach? Equation M2 defined S in the following way:
![]()
N9. Theorem L provides us with an alternate expression for the Changes Series.
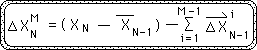
N10. As such, we can write the M+1 term in the S series in the following manner, a combination of N10 and N11. What is the limit of this expression, as N approaches infinity.
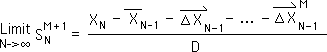
N11. All the identical elements in the Number String Data Stream equal A by definition. Hence, XN also equals A. Theorem I states that as N approaches infinity, the Number String's Living Average, XN bar, approaches A as a limit. Theorem J states that the Number String's Directional, XN arrow, approaches 0 as a limit. Equation N3 assumed the Number String's Mth Directional also approaches 0 as a limit. We make these substitutions in the above equation. This is the result.
![]()
N12. If Equation N3 is true, it is evident that as N approaches infinity that the S term also approaches 0 as a limit.
![]()
N13. Let's apply the above result to Equation N9. We see that the beginning of the right hand side of this equation equals 0 just as does the end of the equation. In other words, the assumption that the Mth Directional approaches 0 as N approaches infinity implies that the next Directional (M+1) also approaches 0 as a limit.
![]()
N14. We induced a pattern from some particular examples. We showed that the inherent logic behind the pattern produced the next member in the series by logical necessity. Our inductive proof is complete. This analysis elevates our inductive pattern to a deductive theorem. Theorem N states: as N approaches infinity, all the Number String's Directionals approach 0.
![]()
Proof O. The Number String's Directionals = Number String Content * Constant
O1. In this section, we prove that each of the Number String's Directionals equals the content of the Number String multiplied by a Constant that is independent of the Number String's content. This relationship is shown in the following algebraic notation.
![]()
O2. Our constant, C, is a function of D, the Decay Factor, nothing else. We give our C subscripts and superscripts to indicate that our constant, C, has a unique value. The number of the Directional, the superscript M, and the place in the data stream, the subscript N, determine this unique value.
![]()
O3. In other words, our constant, C, is not a function of A, the Number String's content. This fact is of utmost importance and is the point of the proof. Note that K, the Scaling Factor, is not another constant. Instead K is a function of D and so does not add a new element to our computations. We have employed K to simplify our algebraic notation.
![]()
O4. We utilize another inductive proof to establish the truth of our initial proposition, Eq. O1. We have already provided specific examples where this relationship is true. Equation H3 shows that the Living Average, XN bar, the original Directional (M=0), is the product of A, the Number String's content, and a constant. Equation H6 shows that the 1st Directional, XN arrow, (M=1), is also the product of A, the Number String's content, and another constant. The equations are shown below.
![]()
![]()
O5. The pattern is clear. To establish the validity of the pattern, we need to show that the logic of the pattern always produces the next element in the series. In other words, if the equation for the Mth Directional, O1, is true, then the following equation for the M+1 Directional, O5, is also true by necessity.
![]()
O6. Theorem M provides an alternate expression for the Mth Directional. In words, the Mth Directional is a sum of the product of K and S. As mentioned, K, the Scaling Factor, is a function of D, the Decay Factor. As such it is a constant.
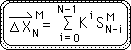
O7. S is a term that we employed to symbolize the first element of the working equation for the Directional, the Change Series divided by D. Theorem L provides another expression for the Change Series. As such S equals the following expression. (Equations N10 through N12 above detail this process.) S has both a superscript and subscript because its value is dependent upon both position in the data stream, N, and the number of the Directional, M.
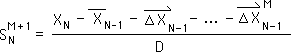
O8. The data stream's content is represented by XN, the 1st term on the right hand side of above equation. However, we are only interested the Number String Data Stream, whose identical content is symbolized by A. Equation O4 provides expressions for the Living Average and the first Directional, the 2nd and 3rd terms. For the purposes of this proof, we have assumed Equation O1 to be true. This provides the alternate expression for the final term. We substitute each of these values in the above equation to arrive at the following:
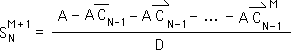
O9. We factor A out of each term in the numerator.
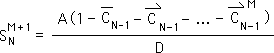
O10. We know that each of our constants, C, are functions of D alone. Hence, S is a product of A and some function of D, i.e. another constant, C. We've given our new constant the same subscripts and superscripts as our S term. Plus we've added an S to indicate its relationship to that term.
![]()
O11. Theorem M, an alternate expression for the Mth Directional, can be expanded in the following fashion, Equation M11.
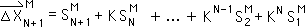
O12. Employing Equation O10, we substitute the appropriate constants, C, for the appropriate S terms into the above expression. This process generates the following:
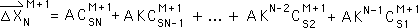
O13. We factor A out of the above equation.
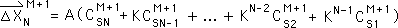
O14. Despite its complicated form, the expression in the parenthesis is a function of D, the Decay Factor. All the K terms, no matter how large their exponents, are functions of D. We know from Equation O10 that all the C terms are also functions of D.
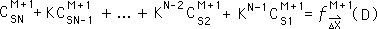
O15. As such, we can write this exceedingly complicated function of D as a constant, C, of the M+1 Directional.
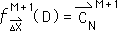
O16. We substitute the above expression into Equation O13 to arrive at the following expression for the M+1 Directional.
![]()
O17. We perceived a general pattern, O1, from some particular instances, O4. To test the validity of this general pattern, we checked to see if the general pattern generates the next term in the series, O5, by logical necessity. Starting from some known theorems and making the proper algebraic manipulations, we arrived the desired result, O5, the next term in the series. Because we have both particular examples and have now established the validity of the logic behind the pattern, we can confidently state that the following theorem is true in all cases. Theorem O: All Directionals of the Number String Data Stream equal the product of the Number String's Content, A, and a constant, C, which is a function of D, the Decay Factor.
![]()